Archive for April, 2020

5 Apr

Lecture: Infinite Sets and Numbers

Posted by hishamuddinz in Advanced Mathematical Physics, Lecture Notes, Mathematics, Sets, Uncategorized.

A set S is said to be finite if there is a natural number n for which S is in one-to-one correspondence with the set N=\{1,2,3,\cdots ,n\}. The set S is then said to have cardinality n i.e. \textrm{card}(S)=n.

Example: For any two sets S,T, the set of all maps \varphi:S\rightarrow T is denoted as T^S. The reason for this notation can be seen as follows. Suppose S,T are finite with cardinalities s=\textrm{card}(S) and t=\textrm{card}(T) respectively. Then \textrm{card}(T^S)=t^s. For instance, the earlier example, we had a (finite) set S and the set of characteristic functions on S having values in the set \{0,1\} is in one-to-one correspondence with the power set 2^S, using the fact that \textrm{card}(\{0,1\})=2.

A set is said to be infinite if it is not finite. But what is infinite? Cantor studied the concept and defined different infinities. This forms the subject of transfinite arithmetic which extends ordinary arithmetic of natural numbers to differentiate their roles of being an ordinal number (how they are ordered in a set) and of being a cardinal number (relating to the size of a set). This allows us to introduce infinities to describe sizes of infinite sets (later).

Natural Numbers

The set of natural numbers \mathbb{N}=\{1,2,3,\cdots\} can be thought as the abstraction of counting. Others will include the number zero and we will use the same symbol \mathbb{N}=\{0,1,2,\cdots\}. If necessary to differentiate for the former, we will write \mathbb{N}^+. The set \mathbb{N} can be built set theoretically as follows:

  • 0=\emptyset ;
  • 1=\{0\}=0\cup\{0\} ;
  • 2=\{0,1\}=1\cup\{1\} ; etc.

With such construction, there exists a unique set \mathbb{N} such that

  • 0\in\mathbb{N} ;
  • n\in\mathbb{N}\Rightarrow n\cup\{n\}\in\mathbb{N} ;
  • The only subset \mathbb{N}' of \mathbb{N} such that 0\in\mathbb{N}' and such that n\in\mathbb{N}'\Rightarrow n\cup\{n\}\in\mathbb{N}' is \mathbb{N} itself.

Some properties of \mathbb{N}:

Proposition: Let n\in\mathbb{N}. Then n=0 or n has a predecessor.

Proposition: Let m,n\in\mathbb{N}. Then m\in n\Rightarrow m\subset n.

Proposition: Let m,n\in\mathbb{N} and let there be a bijection \varphi:n\rightarrow m. Then m=n.

These propositions define ordering for \mathbb{N}. Next, we can define arithmetic operations using set-theoretic operations.

Addition is the map +:\mathbb{N}\times\mathbb{N}\rightarrow\mathbb{N}:: (m,n)\mapsto m+n defined by

m+n=\textrm{card}((m\times\{0\})\cup(n\times\{1\})) ,

or done recursively by

m+0=m,\quad m+1=\textrm{card}(m\cup\{m\}) .

The addition obeys properties like

  • m+(k+1)= (m+k)+1\quad,\quad\forall k\in\mathbb{N} ;
  • m+p=n+p\quad\Rightarrow\quad m=n\ ,\quad m,n,p\in\mathbb{N} .

If m,n,p\in\omega such that n=m+p, then p is called the difference n-m of n and m. The difference n-m exists if and only if m\in n or m=n .

Multiplication is the map \cdot:\mathbb{N}\times\mathbb{N}\rightarrow\mathbb{N} :: (m,n)\mapsto m\cdot n\equiv mn defined by

mn=\textrm{card}(m\times n) .

Note that for now, the symbol \times is reserved for the Cartesian product. The multiplication can be defined recursively for each n\in\mathbb{N} by the following:

0n=0\ ,\quad 1n=n\ ,\quad (k+1)n=kn+n\quad\forall k\in\mathbb{N} .

The multiplication operation further obeys

  • Distributivity over addition: (m+n)p= mp + np ;
  • For any m,n\in\mathbb{N} and p\in\mathbb{N}^+ , mp=np\Rightarrow m=n .

For any n,p\in\mathbb{N}, n is said to divide p or to be a divisor of p if p=mn,\ \ m\in\mathbb{N} .

Exponentiation is the map \mathbb{N}\times\mathbb{N}\rightarrow\mathbb{N} :: (m,n)\mapsto m^n defined by

m^n=\textrm{card}(m^n) .

Note in the above, the right hand side denotes the set of maps n\rightarrow m which has the cardinality m^n. Alternatively, the exponentiation operation can be defined recursively as follows:

m^0=1,\quad m^1=m\quad,\quad m^{k+1}=(m^k)m\quad\forall k\in\mathbb{N} .

Further properties: For all m,n,p\in\mathbb{N} ,

(mn)^p=m^p n^p\ ,\quad m^{n+p}=m^n m^p\ ,\quad m^{np}=(m^n)^p .

Countable Sets

Proposition: The set \mathbb{N} is infinite.

The set \mathbb{N} gives the lowest order of infinity known as countable infinity, sometimes denoted as \omega.

A set S is said to be countably infinite (or countable if the context of infinite set is understood) if S=\{s_0,s_1,s_2, \cdots\} is in one-to-one correspondence with the set \mathbb{N} i.e. there exists a map f such that s_i=f^{-1}(i).

Example: The set of all integers \mathbb{Z}=\{0,\pm 1,\pm 2, \cdots\} is countably infinite. The relevant map f: \mathbb{Z}\rightarrow\mathbb{N} is given by

\begin{aligned} f(0)&=0\\f(n)&=2n-1\\f(-n)&=2n \end{aligned} ,

where n>0.

Theorem: Every subset of a countable infinite set is either finite or countably infinite.

Theorem: The Cartesian product of any pair of countable sets is countable.
Sketch of proof: Let the product be S\times T and their elements of the form (s_i,t_j). Form a sequence out of these elements and map them to \mathbb{N} (see Figure – source: Szekeres). Note that the idea is to ensure that all points are covered before hitting any point at infinity.

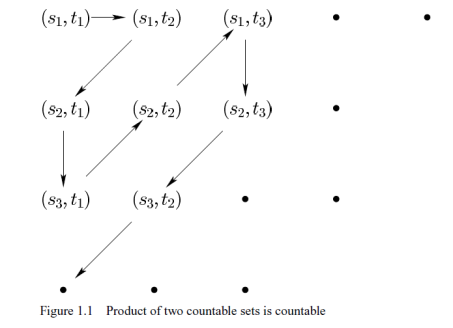
Fig1-1

Corollary: The rational numbers \mathbb{Q} form a countable set.
Note that rational numbers are fractions n/m where n,m\in\mathbb{Z} with no common factors. They are in one-to-one correspondence with a subset of \mathbb{Z}\times\mathbb{N}^+ and hence countable.

Exercise: The subset mentioned above is \mathbb{Z}\times\mathbb{N}^+ modulo an equivalence relation R. What is this relation R?

Earlier, we have seen that the set of real numbers \mathbb{R} is ordered by the relation \le. The set of rational numbers \mathbb{Q} have the property that for any pair of real numbers x,y\in\mathbb{R} such that x<y, there exists a rational number q such that x<q<y. Thus the set \mathbb{Q} is said to be a dense set in \mathbb{R} i.e. real numbers have a countable dense subset.

Uncountable Sets

If a set is neither finite or countably infinite i.e. no one-to-one correspondence with \mathbb{N}, then it is said to be uncountable.

Theorem: The power set 2^S of any countable set S is uncountable.

Proof: Use Cantor’s diagonal argument. Let elements of set S be arranged in a sequence S=\{s_0,s_1,s_2,\cdots\}. Every subset U\subseteq S defines a sequence of 0’s and 1’s as follows:

x=\{\epsilon_0,\epsilon_1,\epsilon_2,\cdots\}\quad\textrm{where}\quad\epsilon_i= \begin{cases} 0\quad\textrm{if}\ s_i\not\in U\\1\quad\textrm{if}s_i\in U\end{cases} .

If 2^S is countable then its elements (subsets of S) can be arranged in sequential form U_0,U_1,U_2,\cdots and hence their sequences

\begin{aligned} x_0&=\{\epsilon_{00},\epsilon_{01},\epsilon_{02},\cdots\}\\ x_1&=\{\epsilon_{10},\epsilon_{11},\epsilon_{12},\cdots\}\\ x_2&=\{\epsilon_{20},\epsilon_{21}, \epsilon_{22},\cdots\}\\ &\vdots\end{aligned}

Let x' be the sequence of 0,1 defined by

x'=\{\epsilon_0',\epsilon_1',\epsilon_2',\cdots\}\quad\textrm{where}\quad \epsilon_i'=\begin{cases} 0\quad\textrm{if}\ \epsilon_{ii}=1\\ 1\quad\textrm{if}\ \epsilon_{ii}=0 \end{cases} .

By the way the sequence x' is defined, the sequence cannot be equal to any sequence x_i since it differs in the i-th place i.e. \epsilon_i'\neq\epsilon_{ii}. The presence of such x' contradicts the assumption that the subsets of S is listable using a unique sequence. Hence 2^S is uncountable.

Theorem: The set of real numbers \mathbb{R} is uncountable.

Proof: Consider [0,1]\subset\mathbb{R} whose elements are expressed as binary decimal:

0.\epsilon_0\epsilon_1\epsilon_2 \cdots\qquad\textrm{with each}\ \epsilon_i=0\ \textrm{or}\ 1\quad(i=0,1,2,\cdots) .

The set [0,1] is uncountable since it is in one-to-one correspondence with 2^{\mathbb{N}}. Hence \mathbb{R} is uncountable.

Earlier: \mathbb{Q} forms a countable dense subset of \mathbb{R}. In contrast, a set is nowhere dense if it is not dense in any open interval (a,b). Example of nowhere dense subset of \mathbb{R} is the uncountable Cantor set. Express real numbers in [0,1] as ternary decimals to base 3 i.e.

x=0.\epsilon_0\epsilon_1\epsilon_2\cdots\quad \textrm{where}\quad \epsilon_i=0,1,2.

Consider those real numbers corresponding to expansion of only 0’s and 2’s. There is a one-to-one correspondence with the earlier binary expansion by replacing 2 with 1. Hence the Cantor set is uncountable. Geometrically, the set can be pictured by the line segment [0,1] and removing the middle third repeatedly (see figure below – source: Szekeres)

Fig1-2

Suppose a Cantor number is a member of the Cantor set.

  • Every real number in [0,2] is the sum of two Cantor numbers.
  • Between any two Cantor numbers, there is a number which is not a Cantor member.

Note that Cantor set is the prototype of a fractal and fractals arise in many places in the natural world and mathematically in many nonlinear maps.

Continuum Hypothesis

Earlier, have mentioned that the countable infinity is the lowest order of infinity. We write the cardinal of the natural numbers as

\textrm{card}(\mathbb{N})=\aleph_0

The symbols \aleph_0, \beth_0 are pronounced as aleph-nought and beth-nought respectively.

The next infinity we encountered comes from uncountable sets. One such set is the real numbers whose cardinality is defined that of a continuum:

\textrm{card}(\mathbb{R})=\mathfrak{c}\equiv 2^{\aleph_0} .

Analogous to finite set S where \textrm{card}(2^S) > \textrm{card}(S), Cantor showed that \mathfrak{c}=2^{\aleph_0})>\aleph_0.

From axiom of choice in set theory (see below), there will be a minimal cardinal number \aleph_1 after \aleph_0. In fact, one can set up a series of ‘infinities’ such that

\aleph_0<\aleph_1<\aleph_2<\cdots .

The continuum hypothesis of Cantor states that the minimal \aleph_1 coincides with the power set of \mathbb{N} i.e.

2^{\aleph_0}=\aleph_1 .

The standing of this hypothesis (and hence the nature of real numbers) remained unknown until Cohen (1966) show that the hypothesis is a genuinely independent axiom, neither provable nor demonstrably false.

Some (brief) comments on axiom of choice is necessary to understand the slippery difficulty of the above problem. The gist of axiom of choice is simply to say that it is always possible to create a set consisting  of a representative element from each set in a family of sets (recall the power set). More formally,

Axiom of Choice: Given a family of sets \mathscr{S}=\{ S_i\vert i\in I\}, there exists a choice function f:I\rightarrow\cup\mathscr{S} such that f(i)\in S_i,\ \forall i\in I.

This is correct for finite and countably infinite families of sets but remains unknown for uncountably infinite sets.

A more commonly used form for the axiom (necessitating a choice function) is given as below:

Zorn’s Lemma: Let \{P,\le\} be a poset with the property that every totally ordered subset is bounded above. Then P has a maximal element.

Note:

  • Q is totally ordered if x,y\in Q, then either x\le y or y\le x.
  • Q is bounded above if there exists x\in Q such that y\le x for all y\in Q.
  • Maximal element of P is an element z such that there is no y\ne z such that z\le y.

It is to be noted that the problem of understanding of understanding the nature of real numbers does not in practice becomes an obstacle to their applications.

References